Generalised signatures

This post presents a technique for defining more reusable OCaml signatures, helping to maintain consistent APIs with minimal boilerplate. We'll work through a few examples, which you can check out on GitHub.

Indexable containers

Consider the following definition of an iter function for some container type t:

let iter f t =
  for i = 0 to length t - 1 do
    f (get t i)
  done

iter requires only that t comes with functions get and length. Many useful operations can be derived in terms of such indexing functions. To take advantage of this, let's move iter into a functor and provide some other useful operations too:

module type Indexable1 = sig
  type 'a t

  val get    : 'a t -> int -> 'a
  val length : _ t -> int
end

module Foldable_of_indexable1 (I : Indexable1) : sig
  open I

  val iter      :        ('a -> unit) -> 'a t -> unit
  val iteri     : (int -> 'a -> unit) -> 'a t -> unit
  val fold_left : ('acc -> 'a -> 'acc) -> 'acc -> 'a t -> 'acc
  val exists    : ('a -> bool) -> 'a t -> bool
  val for_all   : ('a -> bool) -> 'a t -> bool
  val is_empty  : _ t -> bool
  (* ... *)
end

For many types, including array, the get-based definitions are identical to their hand-optimised equivalents (modulo functor application). We can imagine avoiding a lot of standard-library boilerplate – and potential for API inconsistency – by using many such functors ¹. We'd end up defining exactly one iter function that suffices for all Indexable types.

All good so far. Now, let's consider the string type.

A string is also an indexable container with length and get functions, albeit one that can only contain char values. It's natural to expect to be able to re-use Foldable_of_indexable1 in some way: indeed, our definition of iter above is exactly equal to the one in Stdlib.String.iter. Unfortunately, our Indexable1 module type can only describe parametric containers:

module _ : (Indexable1 with type 'a t := string) = Stdlib.String

Error: Signature mismatch:
       ...
       Values do not match:
         val get : t -> int -> char
       is not included in
         val get : t -> int -> 'a
       File "string.mli", line 52, characters 0-57: Actual declaration

We're unable to tell the type system something like

'a t = string    implies    'a = char

as part of our substitution. This means that many types – including string, bytes, unboxed arrays and unboxed vectors – can't benefit from our Foldable_of_iterable1 definitions, even though their own definitions will be identical!

When we wrapped our code in the Foldable_of_indexable1 functor, we needed to give it specific input and output module types, and the ones we picked artificially limited its usefulness. This is a hazard of functorising highly-generic code. As ever, we could solve the problem with copy-paste: a new Indexable0 module type for non-parametric containers, and a new functor Foldable_of_indexable0 with exactly the same implementations as our previous one.

(* Non-parametric indexable types *)
module type Indexable0 = sig
  type t
  type elt

  val get    : t -> int -> elt
  val length : t -> int
end

module Foldable_of_indexable0 (I : Indexable0) : sig
  (* All with the same implementation as before... *)
end

This definition suffers from the dual problem when we try to apply it to parameterised containers like 'a array:

module _ : (Indexable0 with type t := 'a array) = Stdlib.Array

Error: The type variable 'a is unbound in this type declaration.

This time, we wanted to be able to say something like

elt = 'a    implies    t = 'a array    (where 'a is universally quantified),

which is even more nonsensical than our previous attempt. Neither Indexable0 nor Indexable1 can be expressed in terms of the other. We need something more general.

Something more general

Interestingly, it's possible to generalise Indexable0 and Indexable1 with another layer of indirection by making elt a type operator:

module type IndexableN = sig
  type 'a t
  type 'a elt

  val get    : 'a t -> int -> 'a elt
  val length : _ t -> int
end

elt carries the type equalities needed for the Indexable1 case, without forbidding the non-parametric implementation needed for the Indexable0 case. Arrays can set 'a elt := 'a, and strings can set 'a elt := char. Indeed, we can do this in the general case:

(** [Indexable0] is a special-case of [IndexableN] *)
module Indexable0_to_N = functor
  (T : Indexable0) ->
  (T : IndexableN with type 'a t := T.t and type 'a elt := elt)

(** [Indexable1] is a special-case of [IndexableN] *)
module Indexable1_to_N = functor
  (T : Indexable1) ->
  (T : IndexableN with type 'a t := 'a T.t and type 'a elt := 'a)

Now we can define a single Foldable_of_indexableN functor (with exactly the same implementations as before), and it will work for polymorphic and monomorphic containers. Neat!

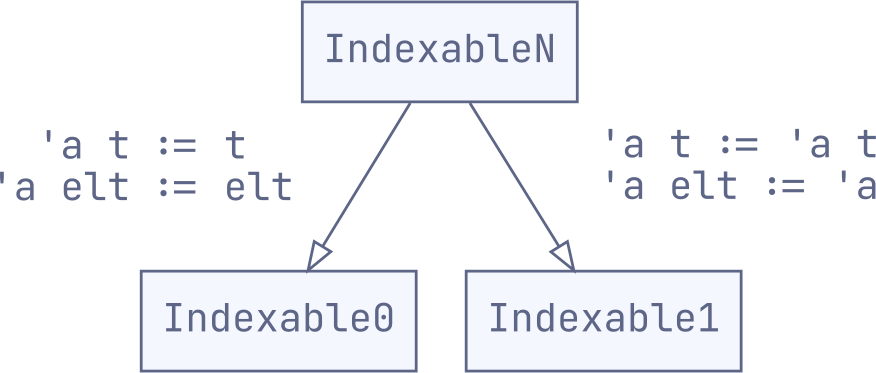
In the general case, when you notice that different signatures are sharing common functions, it's often possible to unify them under a common interface with the following two steps:

1. generalise. Convert pure type variables into type operators (as in 'a → 'a elt), to support use-cases like instantiating those variables to fixed types. Add type parameters to existing types to carry type equalities between them (as in 'a t / 'a elt), to support use-cases where these types depend on each other.

2. specialise. Use destructive substitution (:=) to eliminate those types and type parameters when they're not needed. We're taking advantage of the more powerful destructive substitution offered by OCaml 4.06, which allows us to freely undo our generalisation step.

The truly magical part of this trick is that – with better support for destructive type substitutions recently added to Odoc – it can be made completely invisible² in documentation!

module type Indexable1 = sig
  type _ t

  val get : 'a t -> int -> 'a
  val length : _ t -> int
end

(** This module gets identical documentation to the one above! *)
module type Indexable1' = sig
  include IndexableN with type 'a elt := 'a (** @inline *)
end

What's the cost?

One unavoidable limitation is in what sort of operations we can put in the Foldable_of_indexable functor. Suppose our initial attempt at generalising containers included a sum function:

let sum : int t -> t = fold_left ( + ) 0

sum requires a container that can hold int values, which is clearly not possible for strings as the type system will happily tell us:

   |   let sum = fold_left ( + ) 0
                           ^^^^^
Error: This expression has type int -> int -> int
       but an expression was expected of type int -> 'a elt -> int
       Type int is not compatible with type 'a elt

To state the obvious, we can't rely on parametricity in our container functions if we want them to work on non-parametric containers. The natural solution here would be to define such parametric-only functions in a separate functor.

Other examples

Indexable containers aren't the only example of generalised signatures in the real world. Indeed, many other data-structures and design patterns have APIs that can be unified in this way. Consider the case of hashtables, which have a huge space of possible implementations:

• key types can be left polymorphic by using a magic hash function like caml_hash (as in Stdlib.Hashtbl), or fixed by a user-specified hash function (as in Stdlib.Hashtbl.Make).

• value types can be left polymorphic, fixed by the user (as in persistent hashtables like Index), or even determined by the keys used to index them (as in universal maps like Hmap).

Initially, it looks like these different hashtables will each require their own hand-written signature (and this is what the standard library does with its hashtables). However, with enough type parameters, these different implementations can all be unified under a single Hashtbl_generalised module type:

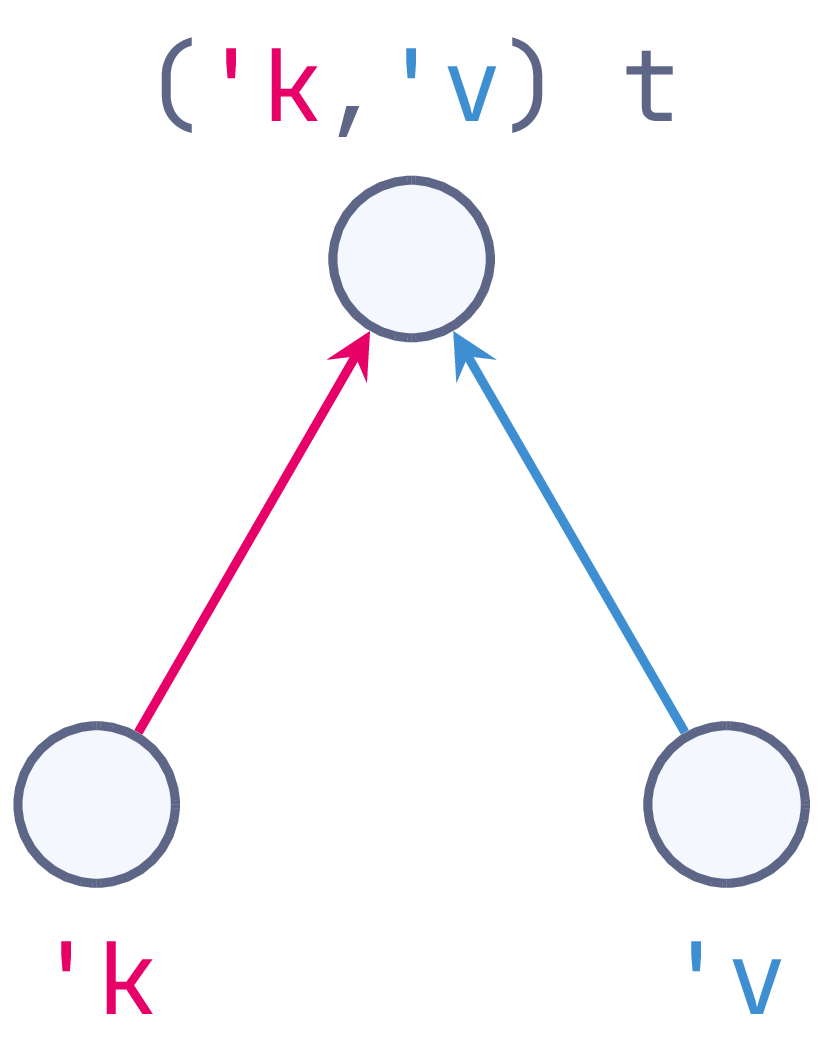
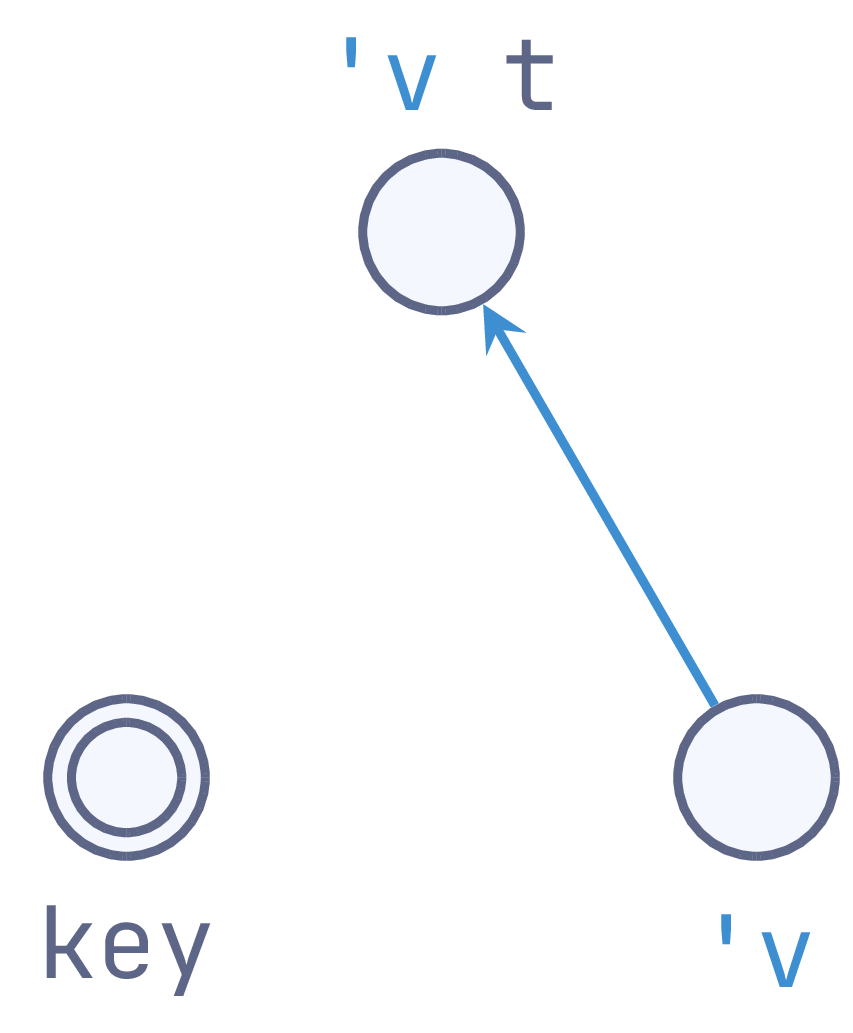
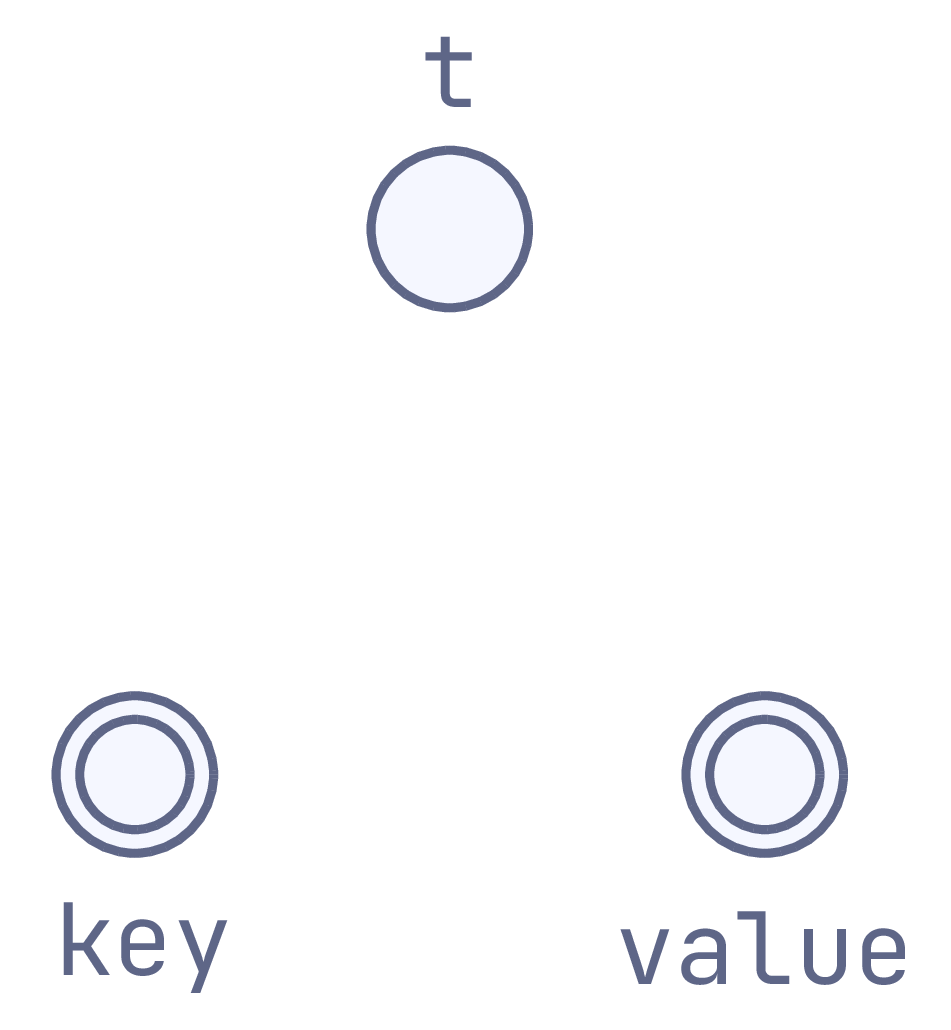
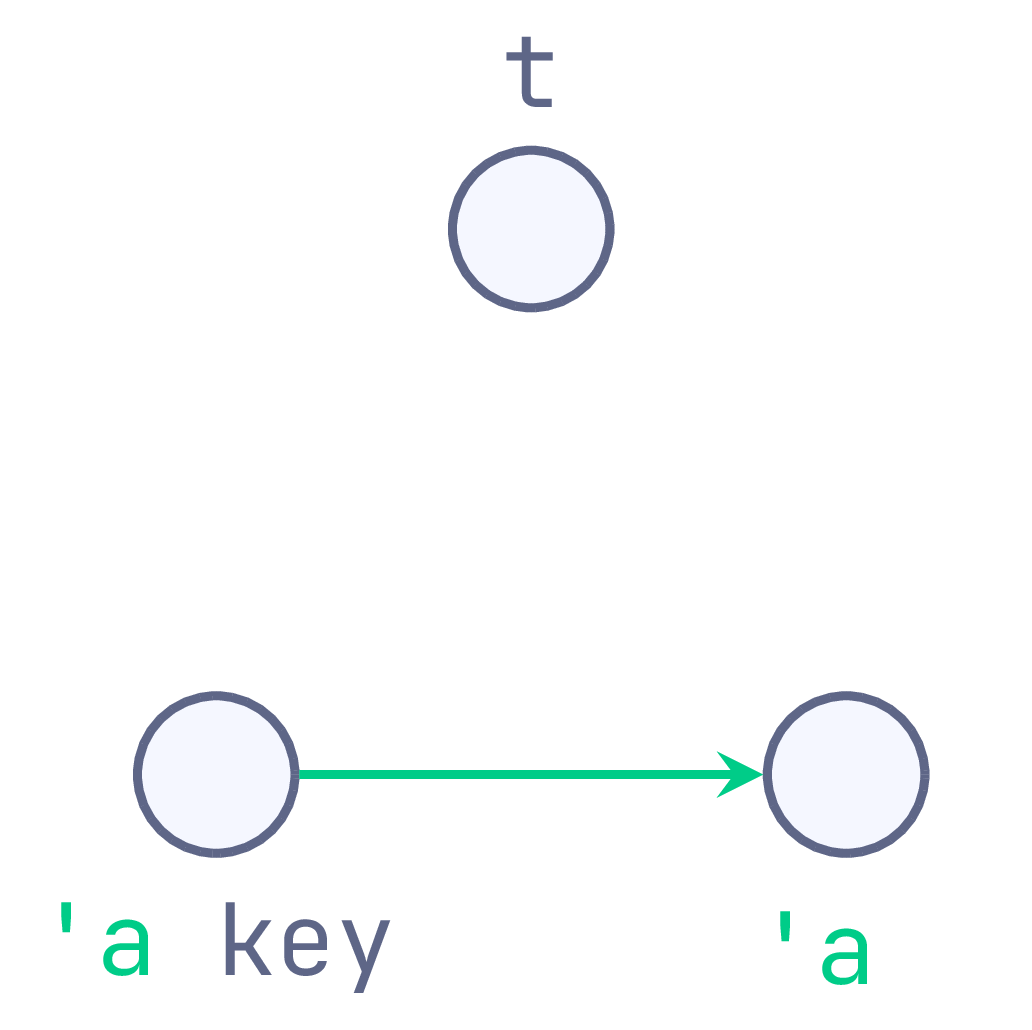
module type Hashtbl_generalised = sig
  (** We have three types ([t], [key] and [value]) and three type variables:

      - ['k]/['v] allow the hashtable to determine key/value types;
      - ['a] is carried from keys to corresponding values, allowing the key to
        determine the types of values. *)

  type ('k, 'v) t
  type ('k, 'a) key
  type ('v, 'a) value

  val create : int -> (_, _) t
  val replace : ('k, 'v) t -> ('k, 'a) key -> ('v, 'a) value -> unit
  val remove : ('k, _) t -> ('k, _) key -> unit
  val find_opt : ('k, 'v) t -> ('k, 'a) key -> ('v, 'a) value option
  (* ... *)
end

We can then implement our different hashtable signatures as specialisations:

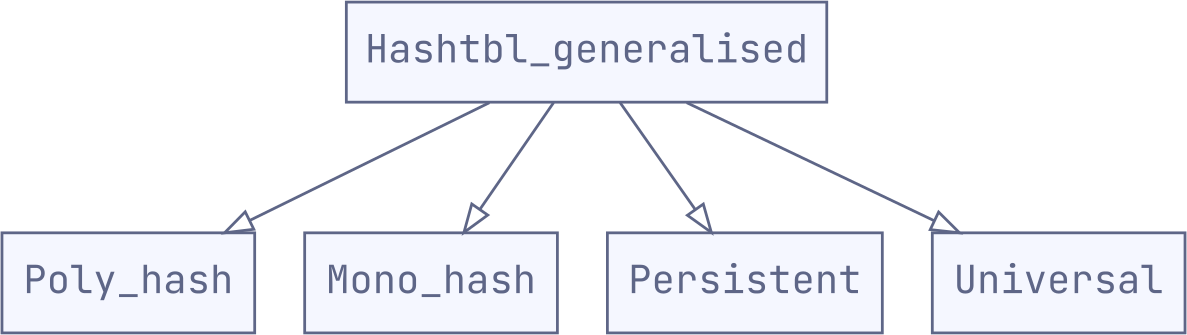
For instance, for the regular polymorphic hashtable:

module type Poly_hash = sig
  include Hashtbl_generalised
    with type ('k, _) key := 'k
     and type ('v, _) value := 'v (** @inline **)
end

The other specialisations are very similar (see here for the specifics).

What is it that makes Hashtable_generalised a good parent interface for these four flavours of hashtable? To get some insight, we can notice that each of the type parameters ('k, 'v, and 'a) connects its own pair of types:

hashtbl_generalised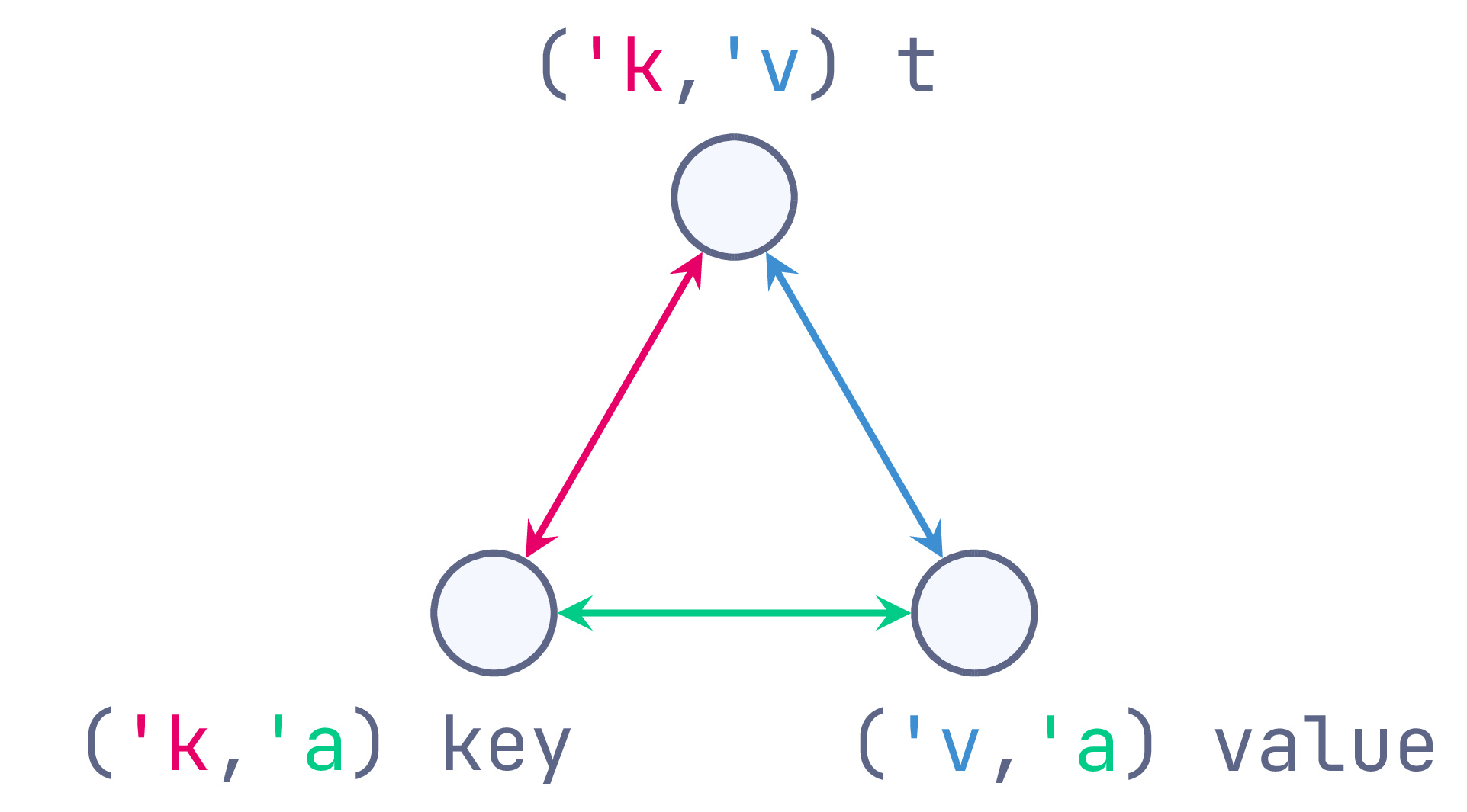

Framed this way, the type parameter 'k exists solely to carry type information between hashtables and their keys (using a type equality at call sites). Similarly, 'v bridges between hashtables and values, and 'a between keys and values. From here, each of our hashtable variants uses destructive subsitution (:=) to prune away unnecessary bridges and express some sort of dependency relation between the types:

poly_hash Keys and value types constrain t at call-sites.	mono_hash The value type constrains t, but keyis fixed by a functor.
persistent Both key and value types are fixed by a functor.	universal Each key's type constrains the corresponding value's type.

In this case, it's not feasible for all these data structures to share the same implementation, but it's still valuable for them to implement a common core API: it ensures consistency of the user-facing functions, allows sharing of documentation, and may even allow these implementations to share a common test suite.

Conclusion

The full code for our Indexable and Hashtbl examples, including explicit definitions of each of the module types, can be found in the generalised-signatures repository. This repository also contains and a third demonstration of this technique being used to express monad-like signatures. The auto-generated documentation for these examples can be viewed online.

Appendix A: Haskell suffers too

The typeclasses in Haskell's base have the same "polymorphic-instances-only" property as our Indexable1 signature (unsurprising, since it doesn't provide any unboxed container types).

class Indexable1 f where        -- Polymorphic instances only
  get    :: f a -> Int -> a
  length :: f a -> Int

A similar trick can be performed there to generalise the typeclass instances for monomorphic containers like Text:

{-# LANGUAGE TypeFamilies #-}

type family   Elt container     -- Relate containers to their element type
type instance Elt [a]  = a
type instance Elt Text = Char

class IndexableN c where
  get    :: c -> Int -> Elt c
  length :: c -> Int

instance IndexableN [a] where   -- Polymorphic instance
  get    = (!!)
  length = Prelude.length

instance IndexableN Text where  -- Monomorphic instance
  get    = Text.index
  length = Text.length

As in the OCaml version, we use an Elt type operator to carry the equality needed for the monomorphic case. This time we used type families to specify the relations explicitly, but we could have used multi-parameter type classes for something more akin to the OCaml functor implementation. See the mono-traversable package for more of this sort of trickery in Haskell.